7-基本情形的参数推断

单个总体均数

f3bi9
即在实际情况下σ（标准差）未知，则使用t变换，用S（样本标准差）
带有自由度（样本量减一）。

t分布特征

单样本t统计量的稳健性
6vogb

1、总体均数的置信区间估计
1）、当总体标准差未知，且样本量n不大时
使用t界值
2）、当总体标准差未知，且样本量n足够大时
近似正态分布，使用z界值

2、总体均数的假设检验
1）建立检验假设，确定检验水准
2）计算检验统计量
3）确定P值，做出判断

1、配对总体差值的置信区间估计（公式一致）

2、配对T检验
1）适用于配对设计的定量数据的两样本均数比较
2）公式一致

1、非参数统计法

2、蒙特卡洛模拟参数推断方法
1）置换法
2）自助法
3）刀切法

3、数据转换法
转化为正态分布数据，再将置信区间逆转化还原

1、两样本均数之差的抽样分布
1）随机样本x1和x2相互独立且服从正态分布，则统计量x1-x2也服从正态分布
2）统计量做标准变化后，统计量服从正态分布
3）用样本标准差s1和s2代替总体标准差后，统计量服从t分布

2、两样本均数之差的t统计量
N<15，需来自正态分布总体才能用t分布
15< N <40 除有离群值或呈强偏态分布，都可用t分布
N >40 近似正态分布，可用t分布

3、两样本均数差值t统计量比单样本t统计量更稳健

1、两总体方差相等
自由度=n1+n2 -2
2、两总体方差不相等
需校正自由度
两种情况下，自由度计算和标准差的计算不同

1、数理定理
1）两样本方差之比的F统计量服从F分布
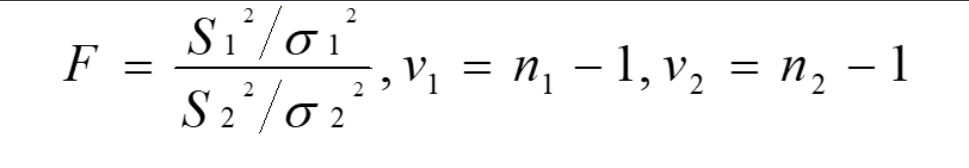
633jn
2）F分布是一种连续性分布，在给定分子自由度和分母自由度的条件下即可求出特定F值，绘制密度曲线图

2、F分布的分位数

使用假设检验
统计量变为F分布的分位数

1、二项分布法（查表）
在样本例数较小，且样本率接近1或0时，为方便应用，可直接查表（n<50）

2、正态近似法
irwyf

3、校正样本率的正态近似法

正态近似法
b17ww

1、样本量较大时两样本率之差的正态近似
vtg1s
2、校正样本率的正态近似

1、正态近似法
56ctg
2、校正样本率的正态近似法

qe6kf