4-基本概率理论
概率
一、机会与不确定性
机会:可被用于描述我们对不确定性事物的看法
随机性:用于刻画事件的不确定性
二、概率的定义与基本性质
1、随机现象:在个别试验中结果不能预测,但在大量重复实验后结果展现出一定规律的现象
2、随机事件:使随机现象中的一种结果或者一组结果,使所有可能结果的一个子集
3、概率:度量事件发生的可能性大小的数量指标称为概率。随机现象中的概率可被定义为随机实验无限重复中随机某事件所占比例
4、概率基本性质:
取值0~1
所有可能结局加起来概率必须等于1
两个事件互斥——加法原则
三、事件的概率运算
1、加法法则
需要是互斥事件
2、条件概率
独立事件:事件A是否发生对事件B发生概率没有影响
条件概率:Pr(A|B)表示条件概率,指在考虑事件B发生的条件下,事件A的发生概率
3、乘法原则
指两个或多个事件同时发生的概率
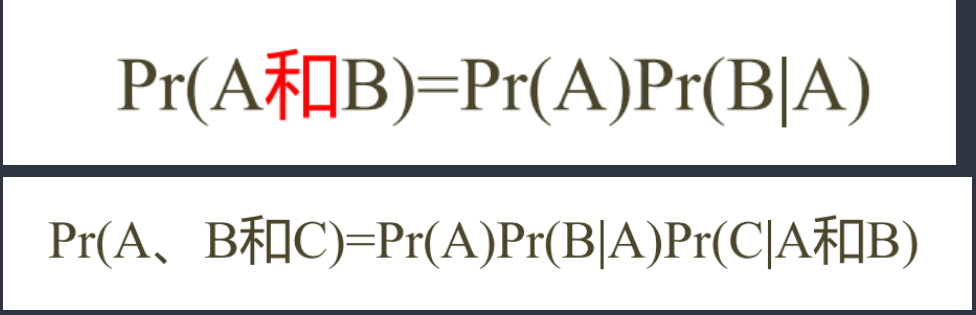
4、条件概率与树状图
概率分布
随机变量:将随机实验中产生的结果用数值表示的变量
一、离散型随机变量
二、连续型随机变量
概率密度曲线
三、随机变量的均数和方差
(1)随机变量的均数
1、离散型随机变量的均数
每个可能的取值与其概率的乘积之和就是所求X的均数:
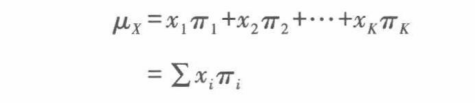
随机变量的均值就是描述总体特征的一个参数(平均数),是一个客观存在的固定数值,不会随抽样样本的不同而发生改变。
2、随机变量之和的均数计算法则
如果X和Y时两个随机变量,随机变量X和Y的和记作Z。则随机变量Z的均数μ等于X的均数加上Y的均数,即X和Y之和的均数,等于X和Y的均数之和。
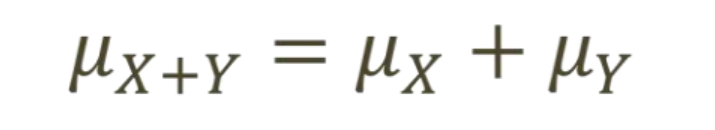
(2)随机变量的方差
1、离散型随机变量的方差


四、二项分布与Poisson分布
(1)二项分布的概念
二项分布:将一个“成功”概率为pi的伯努利实验独立的重复n次,令X表示在这n次实验中“成功”出现的次数,X可能取的值是0,1,2,.......,n,根据n次伯努利实验中“成功”总次数等于k的概率计算公式。得到X的概率分布为:
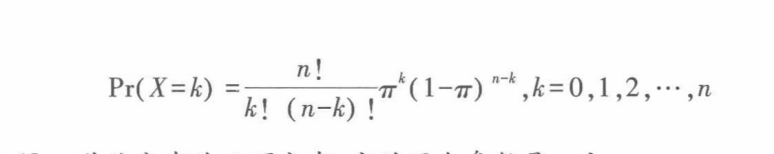
随机变量X服从参数为n和pi的二项分布,常记作X~B(n,pi)
(2)二项分布的性质

(3)二项分布的适用条件
1、互斥性:每次随机试验只会发生两种对立的可能结果之一
2、稳定性:在相同实验条件下,每次实验产生某种结果的概率固定不变
3、独立性:重复实验是相互独立的,即每次实验产生何种结果不受其他各次实验的影响
(4)Poisson分布
Poisson分布常用于稀有事件的发生次数的概率分析。

可理解为概率小,样本大的正态分布
五、正态分布
(1)标准正态分布
定义:均数0,S=1

曲线图:
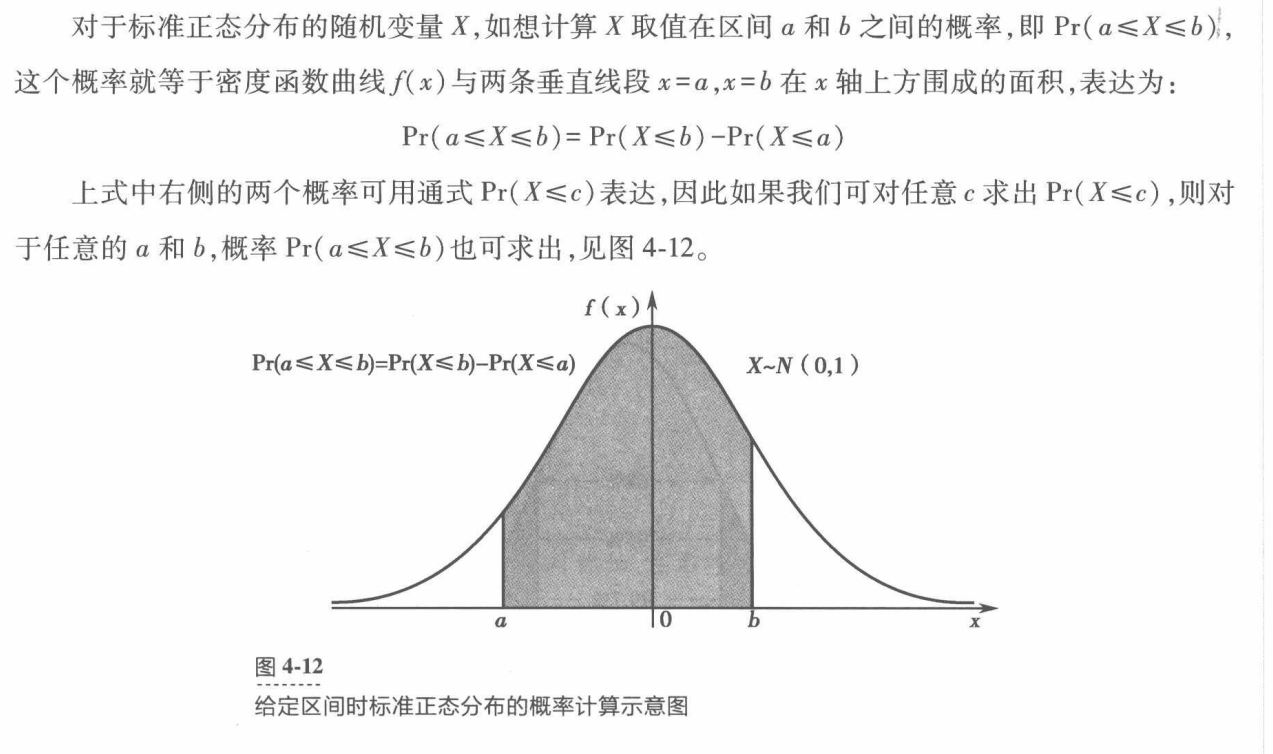
曲线下面积即为X在此取值范围内的概率
标准正态分布曲线下的面积分布规律
- 标准正态分布区间(-1,1),即范围的面积约占总面积的68%
- 标准正态分布区间(-2,2),即范围的面积约占总面积的95%
- 标准正态分布区间(-3,3),即范围的面积约占总面积的99.7%
(2)一般正态分布

正态曲线特点:
1、曲线形状为单峰、钟形,以均数μ为对称轴,左右对称
2、x=μ时,正态分布概率密度函数取得最大值,两边逐渐减少
3、曲线尾端不与横轴相交
4、曲线由μ和σ两个参数决定,μ决定峰值位置,σ决定形状
一般正态分布的转换

即将均数变为0,标准差变为1,变成标准正态分布。

观测值分布是按照均值的位置和距均值位置之间的标准差而定的。
3σ准则
距均值2σ的作为实验观测值的上下警戒线
距均值3σ的左右实验观测值的上下限
(3)正态分布的重要性
1、正态分布能够很好地描述一些实际数据的分布,比如生物的许多特征、测量误差、考试得分等
2、正态分布可以很好地近似许多随机事件的结果,比如多次投掷硬币的结果
3、正常人体的很多生物学指标服从正态分布,可以利用正态分布制定这些指标的“医学参考值范围”
4、根据68、95、99法则,可以制定相应的质量控制线和警戒线
5、建立在正态分布基础上的很多统计推断过程也适用于其他近似对称分布